Sigsegv2 final

Crypto

RektSA 1 vs 100 carottes

Writeup par plean

Ce challenge est dans la continuation du RektSA, challenge de crypto des qualifications. En plus de demander à ce qu’on retrouve d, ce challenge demandait à ce que l’on retrouve aussi p et q.

La partie permettant de trouver phi puis d ayant déjà été expliqué dans plusieurs writeups je ne la réexpliquerai pas, celui-ci par exemple utilise la même méthode que moi pour trouver d et phi.

Une fois phi trouvé on peut en déduire p et q.

Comme nous connaissons r nous pouvons simplifier le problème en factorisant N / r. Pour ce faire nous utiliserons la définition de l’indicatrice d’Euler:

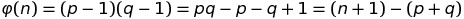
Nous pouvons donc écrire:

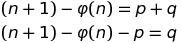
Nous savons d’après RSA que:

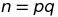
En ramplaçant q par (n + 1) − φ(n) − p nous pouvons déduire que:

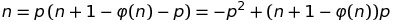
En réarrangeant un peu on trouve:

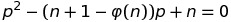
Ceci est une équation quadratique en p, avec:

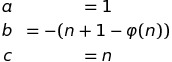
Ce qui peut être facilement résolu en utilisant la formule quadratique:

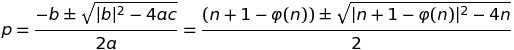
Les deux solutions pour p seront les facteurs premier de n, p et q.

Une fois implémenté notre code ressemblera à ça:

	gmpy2.get_context().precision=2048
	pq_phi = phi // (r-1)
	Nmr = N // r

	a = 1
        b = -(Nmr + 1 - pq_phi)
        c = Nmr

        x = gmpy2.sqrt(gmpy2.mpz(b**2 - 4 * c))
        p = int((-b + x) / 2)
	q = int((-b - x) / 2)

Il nous reste a verifier nos solutions

            assert q * p * r == N
            assert (q-1) * (p-1) * (r-1) == phi

On lance notre script et on récupère le flag :)

$ python3 solv.py
[+] Opening connection to finale-challs.rtfm.re on port 9002: Done
Congratulations: sigsegv{s0_y0u_c4n_s0lv3_1t_w1th_r_4ft3r_4ll...}
[*] Closed connection to finale-challs.rtfm.re port 9002